The paradox of one-sided vs. two-sided tests of significance

Author: Georgi Z. Georgiev, Published: Aug 6, 2018

A lot of people find as paradoxical the claim that a one-sided test of significance at a given p-value offers the same type I error guarantees as a two-sided test that produced the same p-value. Similarly, it is found paradoxical that a one-sided confidence interval at a given significance level has the same coverage probability as a two-sided interval at the same significance level.

The paradox for the significance test can be briefly stated as:

Given the outcome of a randomized controlled experiment for the effect of some intervention one can reject the claim that there is no difference between the treatment and control group in one direction with less uncertainty than one can reject the claim that there is no difference between the two groups at all.

How can one be less certain that there is any difference than that there is difference in a specified direction? Or as Royall ^[1] puts it: how can we conclude neither A nor B, but not conclude "not-A" (see "Solving Royall’s version of the paradox" below). From this paradoxical understanding of the relationship between one-sided and two-sided tests follow a lot of misconceptions and misunderstandings hence why it is important to address it.

Detailed example of the "paradox"

We are using a randomized controlled experiment to test/estimate the effect of an intervention on a given population by drawing two random independent samples of equal size n from it: A (control group) and B (treatment group). Let us say that we have determined that the absolute difference between the means of some characteristic of group A and group B is a good measure for the effectiveness of our intervention. Therefore, if we denote the mean of A with µ_A and the proportion in B as µ_B we are in fact interested in estimating δ = µ_B – µ_A and the uncertainty inherent in that estimation.

Assuming the standard deviations of µ_A (σ_A) and µ_B (σ_B) are known or estimated, we can calculate the pooled standard error of the mean σ_δ. Using the Central Limit Theorem, we know that the standard error is asymptotically normally distributed, so we can calculate critical regions for the standardized Z statistics (or T statistic for small sample sizes) corresponding to a subjectively determined acceptable level of type I error: α.

If we state our hypothesis test as follows:

H₀: δ = 0

H₁: δ ≠ 0

then we are working with a point null and a two-sided alternative hypothesis. We define two critical regions, each on one tail of the normal distribution and each corresponding to α/2. If we take the commonly used value of α = 0.05, and a normal distribution (Z) this results in critical values of -1.96 and +1.96 for the Z statistic. That is, we would reject H₀ only if Z < -1.96 or Z > 1.96.

At the same time, if we state our hypothesis test as follows:

H₀: δ ≤ 0

H₁: δ > 0

then we are working with a null covering one side and zero, and a one-sided alternative. The critical region corresponding to α = 0.05 is defined by Z > 1.6449.

After observing a Z score of 1.81 under a two-sided hypothesis (point null of no difference) we cannot reject the null (1.81 < 1.96). However, if we are interested in rejecting a one-sided null / accepting a one-sided alternative hypothesis we can reject the null with a fair amount of comfort (1.81 > 1.6449).

For many the above is enough to conclude that a one-sided test is less-trustworthy and leads to claims that one-sided tests produce more false positives, more type I errors, biased results, that they have insufficient rigor, that they are less stringent etc. when compared to two-sided tests.

This is not the case, however as both tests provide the same error guarantees against an incorrect rejection of the null hypothesis, at the specified level α . This is despite the fact that if reporting exact probabilities (as one should) the p-value for the one-sided test will be smaller than that of the two-sided test.

Resolving the one-sided paradox

Any paradox can be resolved by examining the premises and finding them to be faulty or imprecise. The one-sided vs. two-sided test paradox is easy to solve once one defines their terms precisely and employs precise language.

First, let us adopt proper notation. The statistical hypotheses for the one-sided tests will be denoted by H1 while the notation in the two-sided case will be H2. Therefore, we state the hypotheses for the two-sided case as:

H2₀: δ = 0

H2₁: δ ≠ 0

and for the one-sided case as:

H1₀: δ ≤ 0

H1₁: δ > 0

Restating the sentence that is paradoxical by replacing "the null" with the proper notation, we get:

"After observing a Z score of 1.81 if we are using a two-sided hypothesis (point null of no difference) then we cannot reject H2₀ (1.81 < 1.96). However, if we are using a one-sided hypothesis we can reject the null H1₀ with a fair amount of comfort (1.81 > 1.6449)."

Replacing "the null" with the proper notation allows us to see that there is no real paradox since we refer to different statistical null hypotheses: one in the case of a two-sided vs. another one in a one-sided test of statistical significance. As the p-value is constructed under a different null under which the proportion of possible outcomes that can falsify it has been decreased, a different critical region of the standardized Z statistic has the same probability of being observed assuming a true null.

Put otherwise, with a two-sided alternative, the null is very specific (point null) so more of the possible observations can happen despite it being true, making it necessary to gather more data in order to reject it at a given significance level. With a one-sided alternative, the null is broader and so fewer (half, for a symmetrical error distribution) of the possible observations can happen despite it being true therefore we need less data to reject it at the same significance level.

The same logic is generalizable for the case of a left side alternative (less than) as well as across a variety of statistical tests, including cases where the null includes a difference in one direction, e.g. if the null is that the effect is larger than some value ɛ the null will be H1₀: δ ≤ 0 + ɛ and the alternative H1₁: δ > 0 + ɛ.

The same logic is fully applicable to one-sided intervals vs. two-sided intervals. If one is interested in an upper or lower boundary that limits the true value from above or below with a given probability, then a one-sided confidence interval should be used. If one is interested in an interval covering the true value XX% of the time without caring to make statements about a value being less than or greater than an interval bound, a two-sided one is appropriate.

If you still find the paradox confusing, read on to see the effect of changing the statistical hypothesis in more detail as well as a metaphor putting it in more practical terms.

Changing the statistical hypothesis: effect on sampling space and outcome space

One can change their statistical hypothesis (question, inquiry) and still get a valid result due to the nature of the question asked. Contrary to what some sources claim, there is no need to pre-specify the directionality of the test, nor is a one-sided test only applicable if only outcomes in one direction are possible.

First, we should realize that the question asked does not have any effect on the sampling space. The fact that the researcher is hoping for, expecting or predicting a result in one direction or the other does not affect the possible values of the variable of interest.

The question asked defines how the outcome space is partitioned: it defines which observed values can be used to reject the null with a given level of rigor. In order to preserve a desired (low) probability for falsely rejecting the null hypothesis when it is true, if the null hypothesis is changed the same must happen with the rejection regions for falsifying it. The probability of observing such an extreme result assuming a true null (a.k.a. p-value) remains the same in all cases. This is an illustration of the above statements:

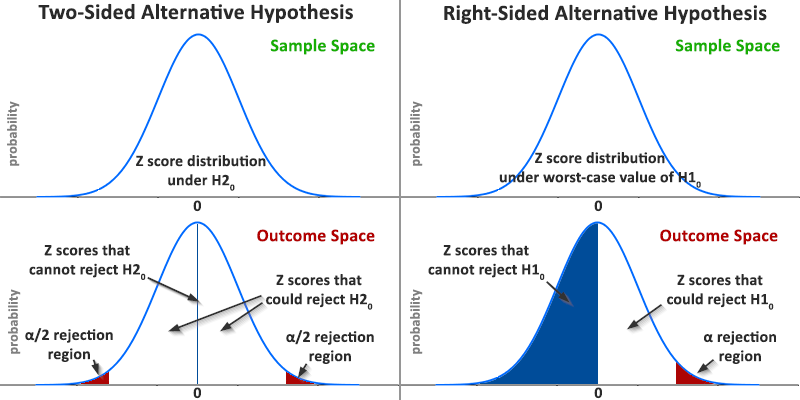
The restriction on the outcome space forces the entire rejection region on one side of the distribution, resulting in a lower absolute critical value of Z. By lowering the critical value |Z| for the one-sided test, the area under the curve continues to reflect the same proportion of the total sample space, thus type I error control is maintained at the nominal level α.

Here is the caveat. Similar to how when testing multiple subgroups, if we find a statistically significant difference in only one subgroup of the population we cannot claim a statistically significant result for the whole population, we cannot turn a directional claim into a general claim for difference at the same significance level or with the same p-value. So, given some datum we can say "we reject that X is worse than or equal to Y, p = 0.01", but we cannot say "we reject that X is not different than Y, p = 0.01". We would need to say "we reject that X is not different than Y, p = 0.02" instead. Narrowing the claim (null hypothesis to be rejected) results in larger uncertainty given the same set of data.

A useful metaphor

I find this weight measurement metaphor useful in illustrating the paradox. Say we have a scale and we know that 68.27% of the time it results in a measurement that is no more than ±1kg off the true weight. Thus, assuming a normal distribution of error, the scale’s standard deviation is 1kg. Suppose the allowed risk for any weight claim we make is 5%, corresponding to 1.644kg critical value for a one-sided claim and 1.96kg critical value for a two-sided claim.

We measure John’s weight and the scale shows 81.8kg. Following this measurement, one can reject the claim "John weighs less than or equal to 80kg" at the 95% significance level (1.644kg < 1.8kg), but one cannot reject the claim "John weighs exactly 80kg" at the 95% significance level (1.96kg > 1.8kg), thus we have the "paradox".

Why is that?

Because under the second claim a scale indication of say 78.2kg, which has a chance to happen due to random error even if John truly weighs exactly 80kg, would count against the null of "John weighs exactly 80kg". The same 78.2kg measurement would not count as evidence against the one-sided null of "John weighs less than or equal to 80kg". In order for the rejection region of the "exactly 80kg" claim to reflect the same error of probability as the "greater than 80kg" claim it has to be adjusted so that the absolute critical value versus that of the one-sided claim is larger.

Note that we can just as easily state that we cannot reject the claim "John’s weight is less than 80kg" at the 95% significance level (the one-sided test in the opposite direction) without any compromise of integrity or validity of the results.

The scale is obviously the statistical test of our choice and it remains uninterested in what claims any of us predicts, expects or wants to make after the weighing. The rest of the metaphor should be obvious.

Solving Royall’s version of the paradox

We can take a slightly different approach in resolving the paradox as presented by Royall (1997): "Statistical Evidence: A Likelihood Paradigm" ^[1]. In a chapter on Fisher’s significance tests, sub-chapter 3.7 "The illogic of rejection trials", Royall tries to use the "paradox" of one-sided vs two-sided tests in arguing against the logic of NHST:

"Thus, a value x for which α/2 < Pr₀(X ≥ x) ≤ α represents strong enough evidence to justify rejecting the composite hypothesis that either θ = ½ or θ < ½, but it is not strong enough evidence to justify rejecting the simple hypothesis that θ = ½. We may conclude (at significance level α) that both θ = ½ and θ < ½ are false, but we may not conclude that θ = ½ alone is false. We may conclude ‘neither A nor B’ but we may not conclude ‘not-A’. Odd."

He goes on by stating it in terms of the alternative hypothesis:

"If, when we reject θ = ½, we are concluding that either θ = ½ or θ < ½, then clearly this is justified by any evidence that justifies the stronger conclusion that θ ≥ ½. That is, if the evidence justifies the conclusion that A is true, then surely it justifies the weaker conclusion that either A or B is true." (emphasis mine)

There is a flaw in Royall’s logic in that he seems to forget that a p-value is a probability calculated under the null hypothesis and it applies only to that specific composite or point null for which it was calculated and no other. One cannot simply break down the null into parts and claim that a rejection of the whole should lead to a rejection of each of the sub-nulls.

It is thus false to say that "We may conclude (at significance level α) that both θ = ½ and θ < ½ are false" if this implies the two statements are treated as separate null hypotheses. Each subset of the null is a null in its own right for the purposes of making inferential claims, thus requires a separate p-value calculation.

By rejecting "θ = ½ or θ < ½" we are not rejecting "θ = ½" (A) and "θ < ½" (B) separately, one after another, but their union as an integral whole ("θ ≤ ½"). Stating this clearly resolves the apparent paradox, as shown below where I examine the two possible logical statements that Royall might have made in a formal way and find that neither leads to the paradox.

The first way to read Royall’s statement "concluding neither A nor B" is as concluding "not (A or B)" (A ∪ B), which is exactly what we do by using a one-sided test. "not-A" (A) does not automatically follow from "not (A or B)" since A ∪ B ≡ A ∩ B (the De Morgan’s laws). There is nothing "odd" about that.

If, however, we translate Royall’s statement to (A ∪ B) instead, then not-A (A) indeed follows from concluding it, but it no longer corresponds to a one-sided test. Furthermore, we do not need any data to conclude (A ∪ B) as it is true by definition since A and B are mutually exclusive in our case: from A ∪ B ≡ A ∩ B we observe A ∩ B to be an empty set and the negation of an empty set is always true so no statistical test is needed to support this claim.

So, if we read Royall’s premise as describing correctly the conclusion of a one-sided test as "not (A or B)" then "not-A" does not automatically follow since B could be false instead. If we read it, ungraciously, as "not A and not B" then we are no longer describing a one-sided test but a situation which does not require any test to make a conclusion. "not-A" is then trivially true, but irrelevant to statistical inference of any kind.

On the graph you can see the logic above represented visually:

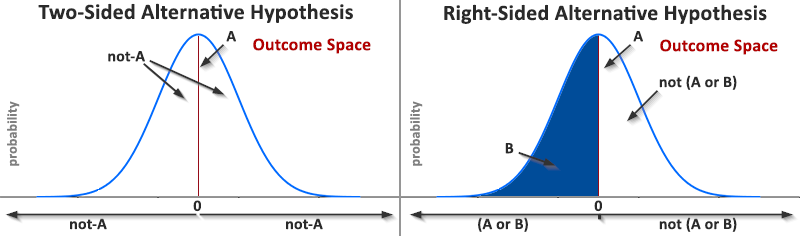
Royall’s logic in the second part of the citation is reversed: it is a stronger (not weaker) conclusion to reject θ = ½ (two-sided test) than it is to reject θ ≤ ½ (weaker, less precise claim, not stronger). This is perhaps due to failure to appreciate that any acceptance of an alternative is a consequence of the rejection of a specific null and it is the precision of the rejected null that determines if a claim is stronger or weaker.

It should be clear from the discussion and graphs that rejecting a point null is a stronger (more precise) statement about where the true effect is probably not, compared to the weaker (less precise) statement that the true effect is probably not in half of the possible values. Rejecting a point null means considering a lot more (double) of the possible observations as evidence against it, while rejecting a one-sided null means considering a lot fewer of the possible observations as evidence against it. Requiring the rejection of a more precise null opens up possibilities to reject it (extends the rejection region in the outcome space) and the critical regions need to be adjusted to account for that.

In terms of the alternatives, accepting a one-sided alternative is a less precise (weaker, not stronger, as Royall states) claim than accepting a two-sided alternative hypothesis. Less precise does not mean less valid, less certain or more suspect, it is just a synonym for "broader", "wider", etc.

Given the above objective statements are easily provable through simple simulations I was driven to search for reasons why this claim seems paradoxical and why there is such stigma against one-sided tests in certain research circles. If you are interested in my thoughts on the subject check out "Is the widespread usage of two-sided tests a result of a usability / presentation issue?"

But what if the result was in the other direction?

This is a question often posed by people who entertain the paradox and so I’ve decided to include a brief comment on it. If the magnitude of the difference in the direction covered by the one-sided null is of no interest, we just fail to reject the null or we can accept the null given that the test had enough statistical power (sensitivity).

If the extent of the difference covered by our original null is of interest, then we can simply reverse the null and alternative and make a claim about an effect in the other direction. In our example we would change H1₀ and H1₁ to be:

H1₀: δ ≥ 0

H1₁: δ < 0

There are no violations of error control in this case, despite some claims to the opposite.

What proponents of such claims seem to forget when they talk about increased errors is that the claim is no longer for H2₀ essentially failing to replace "the null" with the correct statistical hypothesis in the "paradoxical" statement above. If you do that it is only natural that you will continue to worry about the two-tailed non-directional hypothesis while the researcher is only making claims about an effect in one direction, even though it might not be the original direction we expected results in. As already demonstrated, our expectations have no effect on the sample space and thus on the frequency of outcomes. Asking a different question from the same data affects only the outcome space and is thus safe to do without the need for any adjustments or precautions.

If we return to the scale’s metaphor above, we would have done both one-sided tests in sequence and discovered the first one to be non-significant while the second one to be significant. That would have had no effect on the accuracy of the scale or the error measurement associated with whatever claim we decide to make.

I’m grateful to Prof. Daniel Lakens for sanity-checking an earlier version of this article and his useful recommendations.

References

[1] Royall R. (1997) "Statistical Evidence: A Likelihood Paradigm", Chapman & Hall, London, page 77

Enjoyed this article? Please, consider sharing it where it will be appreciated!