Directional claims require directional (statistical) hypotheses

Author: Georgi Z. Georgiev, Published: Aug 6, 2018

A sample of papers from any scientific journal, be it one on physics, economics, psychology, biology, medicine, etc. will inevitably reveal a most obvious truth: people care about the direction of the effect of whatever intervention or treatment one wants to study.

In most published papers and articles, we see claims of "positive effect", "efficacy", "reduces negative effects", "results in reduction of risk", "results in substantial increase in…", "decrease in…", "lowers expenditure", "demonstrate improved…", "shows impaired…" yet we see next to many such claims statements like "All statistical tests were two-sided." or p-values result of calculations under a two-sided alternative (point null) and two-sided confidence intervals.

This is quite peculiar since a two-sided test is a non-directional one and so are two-sided confidence intervals. If we are interested in making claims about the direction of the effect, a one-sided test is clearly the test that corresponds to the questions we are asking, and it is the test which we should adopt to support a directional claim. It is also the uniformly most-powerful test for the directional hypothesis and should be preferred for minimizing type II errors. The nominal type I error associated with the claim is equal to the actual one, unlike when using a two-tailed test, in which case the nominal uncertainty is larger than the actual. For a set of examples of such misuses of two-tailed tests refer to "Examples of improper use of two-sided hypotheses".

This practice leads to results that appear weaker than they are as well as to an increased number of false "negative" findings due to the often-committed mistake of interpreting a high p-value as supporting the null hypothesis without regard for statistical power. Why are then practitioners reporting two-tailed probabilities and why are the statisticians who consult them in favor of such practices?

I believe it is due to a misunderstanding about what a one-sided p-value is combined with the stigma attached to using it from fellow researchers, some journal guidelines and regulatory requirements as well as the unfortunate design of many statistical tables, including the ones provided by Fisher in his 1925 "Statistical Methods for Research Workers" ^[1]. You can see my articles "Examples of negative portrayal of one-sided significance tests" and "Is the widespread usage of two-sided tests a result of a usability/presentation issue" for more on the above.

Here I will examine why one-sided p-values and confidence intervals, and not two-sided ones, are the proper probability to support claims of directional effects.

How to define a statistical null hypothesis

When we engage in reporting a p-value or a confidence interval in a paper, we are performing statistical hypothesis testing, also known as NHST or Null-Hypothesis Significance Testing. Putting the issues of Fisherian versus N-P approaches aside I’ll assume the N-P approach in which we have a null hypothesis and an alternative hypothesis, usually denoted H₀ and H₁.

The statistical null hypothesis should correspond to the default state of matters: in different contexts it may correspond to prior well-established knowledge or to a possible state of the universe we want to reject only if we observe results sufficiently improbable if it were in fact true. In a decision-making context that is usually what corresponds to "no worse than or equal to the currently preferred solution".

If one thinks in terms of arguing or convincing someone, then the null hypothesis will be the argument one will be faced with e.g. "your new molecule is garbage and is in fact worse than or no better than placebo" or "your new medicine is harming people rather than healing them".

In a Fisherian or N-P test we calculate the probability of observing results as extreme or more extreme than the observed, assuming the aforementioned null hypothesis is true – the p-value. In doing so we are addressing the concerns, objections and critiques of any adversary or opponent.

When we observe a statistically significant result and use it as evidence, we are essentially saying: granting your rival theory to be true, we would only see such data in 1 out of N tests performed using this statistical procedure. Thus, we have either seen a very rare and thus unlikely occurrence, or we would have to reject the null hypothesis (and accept the complementary and necessarily composite alternative one). It is the probabilistic equivalent of the logical procedure known as reductio ad absurdum: assuming a premise and then rejecting it after reaching a contradiction*.

Naturally, the choice of N should be such that it appropriately reflects the range of risks and rewards related to making the decision to reject the null hypothesis. The more skewed the balance towards risks, the larger N should be. N should be agreed upon before the experiment that if it produced data of a given level of significance, then the null should be rejected. Our opponent cannot claim that no amount of data can reject their hypothesis as in doing so they would be requiring the impossible (0% uncertainty / 100% certainty). It would be equivalent to conceding that they have an irrational belief which cannot be falsified by any achievable quantity of data.

Note that in all the above the null hypothesis is just a claim. In an experimental scenario it is a research hypothesis to be put to the test, to try to falsify as Karl Popper would say.

So, how should one define the null hypothesis? In most situations, we first define the alternative H₁, which is usually the outcome we hope to see. This is the outcome under which we discover something new and useful, make money, etc. Then the null H₀ is what is left of the sampling space. So, if we really want our new intervention, treatment, device, etc. to be effective, the null hypothesis would be that it is, at best, ineffective, or at worst: does damage, achieves the contrary of what we wanted to achieve with it.

Another approach is to ask: what would an adversary (detractor, opponent or just a sceptic) like to be able say about my intervention, treatment, device, etc.? What would he want to prove as true? And then define this as our null hypothesis (H₀), essentially consenting to their claim in a hypothetical way. Then one can define the alternative H₁ as covering the rest of the possible outcomes.

I do not believe one of these approaches to be better or worse than the other and logically they should result in the same mathematical definitions of H₀ and H_1.

What should be evident from the above is that if one is precise in their definitions there should not be any possibility of conflating the null hypothesis with the nil hypothesis. While the two might coincide in some rare cases, equating them is logically invalid.

What is a directional null or alternative hypothesis?

I should note that when speaking about a directional hypothesis one usually refers to a directional alternative: H₁ for which the complimentary null is also directional but includes zero. For example, H₁: µ₁ > µ­₀ is a right-sided alternative and its corresponding null is H₀: µ₁ ≤ µ­₀. Some refer to such a null as a directional null and I think it is not wrong as long as it is clear that it contains zero. Explicit statement is preferred, though.

Any claim in which a comparison is made between two values (including an observed value and a baseline) that involves stating the exact value of the difference is a directional claim.

While it is often accompanied by qualifying statements such as "is greater than", "is more efficient than", "reduces", "lowers", etc. as already mentioned in the beginning of the article, its presence is not necessary for the claim to be qualified as directional. For example, stating "there is difference between the treatment and control group of 0.4" is already a directional statement since it is referring to γ, not |γ|. I do not think anyone thinks when seeing "0.4" that it could be "0.4 or -0.4" and this is only natural.

Under this definition which I believe to be precise, most, if not all claims made in published research are directional. If you have an example where the absolute value of the difference is of interest and not the observed value, please let me know as I’m blissfully unaware of such cases for now.

Determining which p-value and confidence interval boundary to report

If we want to report a p-value or a confidence interval to support a directional claim we need to consider what is an appropriate null hypothesis under the assumption of which the probability for the interval or p-value is to be calculated. The procedure would be to make the counterclaim and to translate it into a numerical (statistical) form.

For example, if the claim is that a  treatment is more efficient than an existing one, without specifying by how much, then we can use the simple hypotheses: H₀: µ₁ ≤ µ­₀ and H₁: µ₁ > µ­₀.

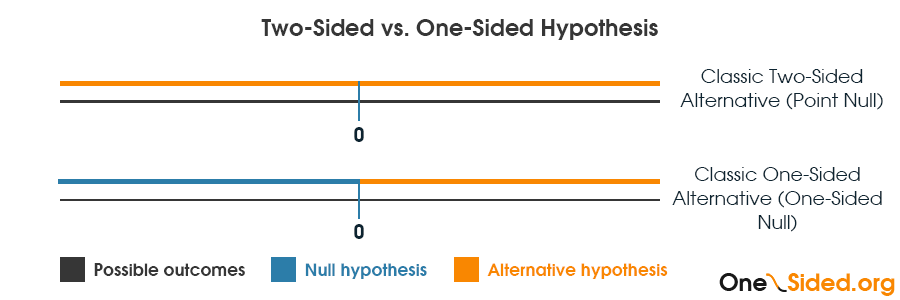
If, however, we want to claim some level of superiority, say that the absolute difference in proportions is 0.2 or that it is 30% better or that it reduces relative risk by 50%, then we should choose our hypothesis more carefully as our critics will now have a different null hypothesis: H₀: µ₁ ≤ µ­₀ + ɛ where ɛ is the claimed level of superiority.

In such a case, if the observed difference is, say, 0.2 and we want to claim a given level of superiority at a given level of certainty (say 95%), then we should take the 95% one-sided interval, for example spanning [0.05, +∞). In this case we can say that we can reject the null that the treatment is less than 0.05 more efficient than the existing one at the 95% significance level and accept the alternative that it is more than 0.05 more efficient. Multiple confidence intervals at different levels of significance can be calculated to support other claims that can be supported with greater or less certainty.

Reporting p-values for directional claims

Given the above, I find the current way of reporting p-values suboptimal and somewhat to blame for the myriad of p-value misinterpretations that we see. Take for example: "the treatment was found to be effective in increasing the survival rate by 0.2 (p=0.02)". What is the p-value calculated for?

Let us denote with δ = µ₁ - µ­₀. Is the reported p-value computed under the null hypothesis of no effect H₀: δ = 0 (1)? Is it for H₀: δ ≤ 0 (2)? Is it for H₀: δ ≤ 0.2 (3)? Each of these nulls results in a different p-value!

Most of the time we would like to know p under (2) and sometimes under (3) for H₀: δ ≤ L_b where 0 ≤ L_b ≤ 0.3 and is some kind of uncertainty bound, but instead we get it computed under (1). Given that, it is hardly surprising that people are confused about how to interpret p-values. If they want (2) then they are seeing a nominal probability which is two times higher than the actual. If they want (3) then most of the time they are seeing a nominal probability which is much lower than the actual.

Some authors have the good sense to report a confidence interval around the observed value. Unfortunately, most of the time it is also constructed under (1) so it is overestimating the error in judgement one would make if they compare values to either interval bound. In such cases the p-value is likely improperly calculated as well (usually under (1)).

Such ambiguities would be avoided to a significant extent if the null hypothesis is explicitly stated next to the p-value. For example: "the treatment was found to be effective in increasing the survival rate by 0.2 (p=0.01; H₀: µ₁ - µ­₀ ≤ 0)" for a simple one-sided hypothesis.

What if we see an unexpected result (in the opposite direction)?

The incorrect matching between a research and a statistical hypothesis seems to be the reason why this question is asked at all. In some cases, the mismatch might be due to incorrect reasoning and in others it could be due to blind application of procedures. Or maybe it is due to the apparent "Paradox of one-sided vs. two-sided tests of significance"?

Whatever the reason, the idea is that according to some if we register a study with a type I error α for a one-sided test in one direction then we should not conduct a one-sided test in the other direction after seeing an unexpected result. Doing so is chastised really harshly and can result in name-calling. Understanding the need for correspondence between a statistical and a research hypothesis combined with the fact that our hypothesis has no impact on the sampling space can help us see through that non-issue.

In a well-thought-out experiment the statistical hypothesis will relate to the research hypothesis in a meaningful manner and support its claim, but they are rarely the same thing, as it would only happen when the research hypothesis is a basic statement about the true value of the parameter of interest.

For example, the research hypothesis might be "Intervention X has a positive effect on population Y (due to A, B, C)". The null hypothesis, or the thing we do not want to dispose of easily, is thus that "Intervention X relying on A, B, C has negative or no effect on population Y". The paper that would be written if the null hypothesis is rejected in the experiment would be titled "Intervention X beneficial for Y".

Translated to a well-defined statistical hypothesis it becomes "Intervention X has a positive effect on some measure Z in population Y". The null hypothesis, or the thing we do not want to dispose of easily is thus that "Intervention X has negative or no effect on measure Z in population Y". The paper that would be written if the null hypothesis rejected in the experiment would be titled "Intervention X beneficial for improving Z in Y". The maximum probability for a type I error would be controlled by conducting a one-sided test of the appropriate form.

However, if it turns out that intervention X demonstrates a negative effect of significant magnitude the most natural thing to do is to conduct a one-sided test of significance in the negative direction. The question is changed and so is the null hypothesis and the paper that would be published if the null is rejected will now be titled "Intervention X harmful for population Y based on measures of Z".

If the question was: "is there an effect of intervention X in the positive or the negative direction" then a two tailed test would be appropriate, however this non-directional question is rarely what interests us. We usually care both about the presence of an effect and its direction, so we care about a narrower set of possible answers to a question broader than the one answered by a two-sided alternative hypothesis.

That such an unexpected results will likely disagree with a lot of published literature and be hard to explain for the researcher and the scientific community has no bearing on the validity of the statistical test that best corresponds to the research claim warranted by the data.

Severe Testing and reporting SEV(claim)

The approach of Deborah Mayo & Aris Spanos ^[2,3] with the severity criterion is trying to address the issue of matching claims and hypotheses in a structured and philosophically defensible way by calculating the severity with which a claim can be made given some data. Informally, a statistical hypothesis or claim can be said accepted only to the extent to which it has passed a severe test, that is, a procedure, which if it was false, would have detected that with high probability.

Severity is a post-hoc test which, like power, is calculated for a point alternative hypothesis and provides an assessment of the uncertainty (error) related to inferences about it. Severity provides error probabilities both when we reject H₀ and when we want to accept it, depending on whether a pre-specified level of significance has been attained.

* Note: D.Mayo & A.Spanos argue for treating it not as reaching a contradiction but as "strong argument from coincidence" when referring to the case at hand and not relying on explanations based on long-run errors or behavior-guiding qualities of procedures (Mayo & Spanos, 2006, 2010) ^[2,3])

I thank Prof. Daniel Lakens for sanity-checking this article.

References

[1] Fisher R.A. (1925) "Statistical methods for research workers". Oliver & Boyd, Edinburg

[2] Mayo D.G., Spanos A. (2006) "Severe testing as a basic concept in a Neyman–Pearson philosophy of induction", The British Journal for the Philosophy of Science, Volume 57-2:323–357; https://doi.org/10.1093/bjps/axl003

[3] Mayo D.G., Spanos A. (2010) "Error statistics", in P. S. Bandyopadhyay & M. R. Forster (Eds.), Philosophy of Statistics, (7, 152–198). Handbook of the Philosophy of Science. The Netherlands: Elsevier; ISBN: 9780444518620

Enjoyed this article? Please, consider sharing it where it will be appreciated!