A p-value is meaningless without a specified null hypothesis

Author: Georgi Z. Georgiev, Published: Aug 6, 2018

This is a brief article arguing against the common practice of reporting a p-value without specifying the null hypothesis under which it was computed, for example:

"the treatment was found to be effective in increasing the survival rate by 0.25 (p=0.02)".

We know that after observing a low p-value, there are three possible conclusions:

1. The null hypothesis is false (reject claim H₀).
2. We have observed a rare outcome.
3. The statistical model does not reflect reality (e.g. wrong distribution used,observations not independent…).

Most of the time we are hoping that #1 is what is true. If it is true, can we state what claim we should be rejecting with a p-value of 0.02 in the above example? What was the hypothesis the p-value is calculated under?

If we use the notation δ = µ₁ - µ­₀ then is the reported p-value computed under the null hypothesis of no effect H₀: δ = 0 (1.)? Is it for H₀: δ ≤ 0 (2.)? Is it for H₀: δ < 0.25 (3.)? Computation for each of these different nulls results in a different p-value, so without knowing which was used do we just proceed with whatever we want to hear?

If one focuses on "increasing the survival rate" then they assume it was computed under (2.). If one looks at the absolute change in survival rates of 0.25 they might be thinking of "increasing survival rate by 0.25" (3.). However, most of the time one is looking at a p-value computed under (1.) due to various reasons, including regulatory, journal and other types of guidelines, as well as misconceptions and misuse of the statistical methods.

How can this ambiguity be avoided?

Specify your null hypothesis

In order to avoid any such confusions among consumers of reported p-values my advice is for researchers to be explicit about the null hypothesis used for the computations by specifying it next to the p-value.

This is a visual representation of the three claims, the third I dub "Substantive" since usually when it is computed it will not be against the observed value, but against a difference from zero considered of practical significance.

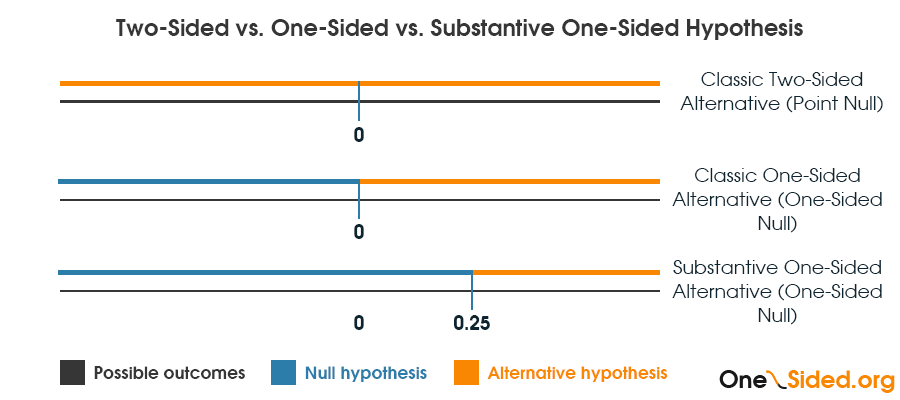
Continuing the above example, this is how the p-value should be reported in each case:

1. "the treatment was found to have an effect on survival rate (p=0.02; H₀: δ = 0)"
2. "the treatment was found to be effective in increasing the survival rate with an observed effect of 0.25 (p=0.01; H₀: δ ≤ 0)"
3. "the treatment was found to be effective in increasing the survival rate by 0.25 (p=0.5; H₀: δ < 0.25)"

As you can see the p-values are very different in each case with p always being equal to 0.5 if inference is made for a one-sided hypothesis bound by the observed value (3.). It is also obvious that a p-value computed in case (1.) would not have corresponded to the claim next to it if I have kept the original claim, which is why I have altered it.

As I have argued, a two-sided p-value should not be reported as supporting a directional claim: a directional claim requires a directional, one-sided test. If you, for some reason, must do it, then at least specify the null under which it was computed, e.g. "the treatment was found to be effective in increasing the survival rate by 0.25 (p=0.02; H0: δ = 0)".

I have also altered claim (2.) so it has less potential to confuse someone that we are in fact computing p under case (3.).

An example with the above data in a tool in which the null hypothesis under which the p-value has been calculated is made explicit can be seen here.

Notation details

I think "H₀:" can be skipped from the notation for brevity, especially if this notation becomes conventional and it us understood that the null is specified after ";".

The reason why ";" is chosen and not "|" is that the probability is not conditional on an event. We are computing a marginal probability under a given assumption. Here I am following the recommendation of Mayo & Spanos (2010) ^[1] for notation in order to avoid confusion. In writing about why P(d(X) ≥ d(x₀); H₀) should not be written as P(d(X) ≥ d(x₀)| H₀)) she states: "It is simply to state what is deductively entailed by the probability model and hypothesis. Most importantly, the statistical hypotheses we wish to make inferences about are not events; trying to construe them as such involves fallacies and inconsistencies".

References

[1] Mayo D.G., Spanos A. (2010) "Error statistics", in P. S. Bandyopadhyay & M. R. Forster (Eds.), Philosophy of Statistics, (7, 152–198). Handbook of the Philosophy of Science. The Netherlands: Elsevier; ISBN: 9780444518620

Enjoyed this article? Please, consider sharing it where it will be appreciated!